이번에는 NAND/NOR로 정규형(표준형) 회로 만드는 법에 대해 알아보겠습니다. 원래는 바로 간소화로 넘어갈까 했지만, 간단하게라도 소개하는 것이 이해하는 데 도움이 될 것 같아 따로 포스팅하게 되었습니다.
혹시 NAND/NOR의 정의와 진리표를 찾아오셨다면 이전 포스팅에서 다루었으니 아래 링크를 참고해주세요.
https://homubee.tistory.com/27
[컴퓨터 구성] #1 논리 게이트(Logic Gates)
오늘은 논리 게이트에 관해 알아보겠습니다. 논리 게이트는 컴퓨터를 구성하는 기본 요소이므로 컴퓨터 구성 공부를 위해 꼭 알아야 할 내용입니다. 자세하게 살펴보도록 하겠습니다. 논리 게
homubee.tistory.com
드 모르간 법칙과 게이트 변환
지난번에 완전 집합을 공부하면서 NAND/NOR로 { AND, OR, NOT }을 만들어 봤었는데요, 매번 그 방식으로 회로를 만들려면 복잡하고 어려우니, 정규형을 가지고 한 번에 NAND/NOR만의 회로를 만드는 방법에 대해 알아보겠습니다.
원리는 아주 간단합니다. 바로 드 모르간의 법칙을 활용하는 것입니다. 직접 회로 모양을 보며 눈에 익히도록 합시다. 먼저 A'B'=(A+B)'입니다. 이에 따라 다음 두 게이트가 서로 논리적 동치임을 알 수 있습니다.

다음은 A'+B'=(AB)'입니다. 이번에도 역시 다음 두 게이트가 서로 논리적 동치임을 알 수 있습니다.
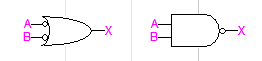
당연한 사실이지만 눈으로 직접 회로를 보는 것과 머릿속으로 생각만 하는 것은 다르므로, 다시 한번 정리해보았습니다.
자 그런데, 이제 이걸로 어떻게 NAND/NOR만의 회로를 만들 수 있을까요? 지금부터 직접 만들어보며 알아보도록 합시다.
NAND 게이트로 설계하기(최소항 활용)
NAND 게이트로 설계하기 위해서는 AND+OR 구조로 되어 있어야 합니다. 따라서 처음 논리식을 세울 때, 최소항으로 SOP를 만들어야 합니다. 저는 지난 포스팅에서 공부했던 정규형 논리식을 그대로 가져왔습니다. f=x'y'z+x'yz+xy'z'+xy'z+xyz 였는데요, 이를 가지고 회로를 설계해보겠습니다. 그대로 만들면 다음과 같습니다. (input의 NOT은 생략하고 ' 기호로만 표시했습니다.)
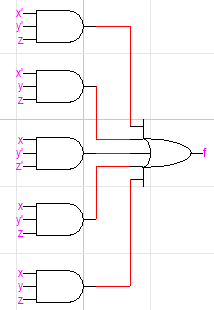
하지만 이건 AND와 OR가 막 섞여 있어서 그다지 좋은 구조가 아닙니다. 따라서 NAND 게이트로 통일하여 다시 설계해보겠습니다. 아까 위에서 봤던 드 모르간 법칙을 활용한 게이트 변환법을 쓰면 됩니다.
그냥 말로는 이해가 어려울 수 있으니 그림을 보며 자세히 설명해드리겠습니다.
1. NOT 붙이기

먼저, 각 최소항으로 구성된 AND 게이트의 앞에 NOT을 붙여줍니다. 일단 대부분 NAND로 바꾸는 데 성공했습니다.
2. 원상복구
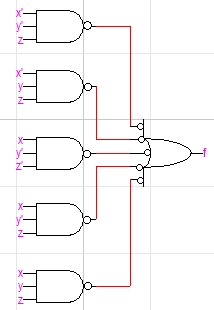
문제는 뒤에 연결된 OR인데요, 일단 NOT을 붙여줬으니 원상복구해야 원래 식으로 돌아오겠죠?(이중부정법칙을 생각해보시길 바랍니다.) OR의 모든 입력에 NOT을 붙여줍니다.
3. 게이트 변환

이제 게이트 변환법을 쓰면 됩니다. 모든 입력에 NOT이 붙은 OR 게이트는 NAND 게이트로 바꿀 수 있습니다.
따라서 모든 게이트를 NAND로 바꾸었고, 이는 NAND로만 설계한 회로입니다. 전체 변환 과정은 아래와 같습니다.



NOR 게이트로 설계하기(최대항 활용)
NOR 게이트로 설계하기 위해서는 OR+AND 구조로 되어 있어야 합니다. 이번에는 처음 논리식을 세울 때, 최대항으로 POS를 만들어야 합니다. 따라서, 아까 위에서 봤던 정규형 논리식의 POS 버전을 가져왔습니다. f=(x+y+z)(x+y'+z)(x'+y'+z) 인데요, 이를 가지고 회로를 설계해보겠습니다. 그대로 만들면 다음과 같습니다. (input의 NOT은 생략하고 ' 기호로만 표시했습니다.)

하지만 이번에도 AND와 OR가 막 섞여서 영 불편합니다. 따라서 NOR 게이트만 가지고 다시 설계해보겠습니다. 이번에도 위에서 봤던 드 모르간 법칙을 활용한 게이트 변환법을 쓰면 됩니다. NAND로 만들 때와 거의 비슷하기 때문에 어렵지 않습니다.
이번에도 그림을 보며 다시 생각해봅시다. 앞선 과정과 같은 단계를 거치면 됩니다.
1. NOT 붙이기

먼저, 각 최대항으로 구성된 OR 게이트의 앞에 NOT을 붙여줍니다. 이번에도 대부분 NOR로 바꾸는 데 성공했습니다.
2. 원상복구

항상 문제는 뒤에 연결된 게이트입니다. 일단 NOT을 붙여줬으니 이번에도 원상복구 작업이 필요합니다. 따라서 AND의 모든 입력에 NOT을 붙여줍니다.
3. 게이트 변환

이제 게이트 변환법을 쓰면 됩니다. 모든 입력에 NOT이 붙은 AND 게이트는 NOR 게이트로 바꿀 수 있습니다.
따라서 모든 게이트를 NOR로 바꾸었고, 이번에도 NOR로만 설계한 회로를 완성했습니다. 전체 변환 과정은 아래와 같습니다.

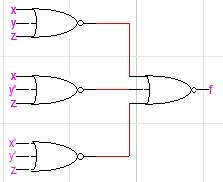
번외편 1: 표준형에서는 어떻게 만들까?
표준형에서 만드는 법도 똑같은데요, 하나 헷갈릴 수 있는 부분이 있어서 그 부분만 정리하도록 하겠습니다.
아마 실제로 회로를 만들 때는 대부분 단순화해서 표준형으로 만들 텐데요, 변수가 하나만 남았을 때, 어떻게 변환해야 하는지 어려워하실 수 있습니다. 예를 들면 f=a+bc'+d'이라는 식을 얻었다고 합시다. 회로는 아래와 같습니다.

bc'는 AND니까 NOT을 붙여서 NAND로 만들면 되는데, a랑 d'은 어쩌죠? 사실 간단합니다. 이때도 똑같이 NOT을 붙여주시면 됩니다. 아래 회로를 참고해주세요.

완전히 NAND로만 만들고 싶으시면 완전 집합 포스팅에서 NAND로 NOT 만드는 법을 참고해주시고, 일단 저는 여러분이 이해하기 쉽게, 그냥 NOT 게이트를 사용했습니다.
사실상 정규형과 똑같은데, 그냥 NOT이 바로 연결되어 있다고 생각하시면 됩니다. NOR도 똑같으니 직접 한 번 해보세요!
번외편 2: XOR, XNOR 설계하기
언젠가 한 번 소개해야겠다 싶었는데, 내용이 짧고 마땅히 넣을 곳도 없고 해서 가장 관련 있는 이번 포스팅에서 소개합니다.
NAND로 XOR 만들기

A⊕B=X는 위와 같이 만듭니다. 불 대수를 적용해보면 쉽게 알 수 있으니 설명은 생략하도록 하겠습니다. XNOR를 만들고 싶으면 끝에 NAND로 만든 NOT을 붙여주면 됩니다.
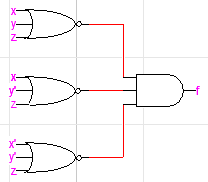
NOR로 XNOR 만들기
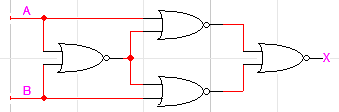
(A⊕B)'=X는 위와 같이 만듭니다. XOR와 마찬가지로 설명은 생략하겠습니다. 이해가 어렵다면 직접 진리표를 만들어보면 도움이 될 것입니다. 이 역시 XOR를 만들고 싶으면 끝에 NOR로 만든 NOT을 붙여주면 됩니다.
사실 A⊕B=AB'+A'B이므로 앞에서 했던 정규형으로 설계하는 방법도 가능하지만(회로 형태는 달라집니다.), NOT을 안 쓰고 가장 깔끔하게 설계할 수 있는 방법이라 이렇게 따로 소개해 드렸습니다.
오늘은 NAND/NOR로 정규형(표준형) 회로 설계하는 방법에 대해 알아봤습니다. 사실 공부하실 때는 그냥 편한 대로 회로를 구성하면 되지만, 실제 회로를 만들 때는 이렇게 NAND나 NOR만 쓰인다는 점을 기억해두시면 좋을 것 같습니다.
다음 포스팅은 식 간소화에 대해 다룰 것 같습니다. 여유가 된다면 카르노맵까지 한 번에 올릴 수도 있고, 너무 길면 나눠질 수도 있습니다.
직접 조사해서 작성하는 글이다 보니 일부 정확하지 않은 정보가 포함되어 있을 수 있습니다.
궁금한 사항이나 잘못된 내용이 있으면 댓글로 알려주세요~
구독과 좋아요, 환영합니다!
'컴퓨터 이론 > 컴퓨터 구성' 카테고리의 다른 글
| [컴퓨터 구성] #7 반가산기(Half Adder), 전가산기(Full Adder) (0) | 2022.09.10 |
|---|---|
| [컴퓨터 구성] #6 카르노 맵 (Karnaugh Map)과 식 간소화 (2) | 2022.08.20 |
| [컴퓨터 구성] #4 정규형(Canonical form)과 최소항(minterm)/최대항(maxterm) (2) | 2022.04.02 |
| [컴퓨터 구성] #3 불 대수(Boolean Algebra)와 기본 법칙 (0) | 2022.03.23 |
| [컴퓨터 구성] #2 완전 집합(Complete Set) (0) | 2022.03.16 |