이번에는 지난 포스팅에 이어 완전 집합에 대해 알아보겠습니다. 크게 중요한 내용은 아니니 부담 없이 가볍게 알아간다는 느낌으로 공부하면 좋을 것 같습니다.
완전 집합 (Complete Set)
완전 집합이란 임의의 논리 게이트를 만들 수 있는 게이트 집합을 이야기합니다. 이렇게 말하면 어려우니 조금 더 쉽게 설명해보겠습니다.
우리가 가장 기본이 된다고 생각하는 게이트 3가지가 있죠? AND, OR, NOT입니다. 특정 게이트 집합이 이 3가지 게이트를 모두 구현할 수 있다면, 그 집합은 완전 집합이라고 할 수 있습니다. 예시를 살펴보며 자세히 알아보겠습니다.
먼저, { AND, NOT } 은 완전 집합입니다. 즉, 이미 AND와 NOT 게이트는 포함되어 있으므로, 이 둘을 이용해서 OR 게이트를 만들 수 있다는 뜻입니다. 이는 불 대수에 의해 간단하게 확인할 수 있습니다. 지금 사용할 수 있는 것은 ' (NOT)과 · (AND, 이하 기호는 생략) 뿐이므로, 이를 잘 조합하면 (a'b')' = a+b 와 같은 식을 얻을 수 있습니다. NOT과 AND만 사용하였지만, OR 게이트를 구현하였습니다. 따라서 이는 완전 집합이라고 할 수 있습니다.
{ OR, NOT } 또한 완전 집합입니다. 이번에는 OR과 NOT으로 AND 게이트를 만들어보겠습니다. (a'+b')' = ab 이므로, AND 게이트를 구현하였습니다. 따라서 이 역시 완전 집합이라고 할 수 있습니다.
(드모르간 법칙을 생각해보면 이해가 쉽습니다.)
NAND 게이트와 NOR 게이트
지난번에 NAND 게이트와 NOR 게이트는 그 자체로 완전 집합이 된다고 소개했습니다. 즉, { NAND }, { NOR } 모두 완전 집합입니다. 이 부분 역시 불 대수를 통해 확인할 수 있지만, 이번에는 직접 게이트를 설계하여 AND, OR, NOT을 모두 만들어보도록 하겠습니다.
NAND
본격적으로 들어가기에 앞서서 잠깐 진리표를 다시 살펴보겠습니다. NAND는 입력이 모두 1일 때만 출력이 0인 게이트입니다. 아래의 진리표와 비교해가며 각 게이트를 구현해보겠습니다.

- NOT
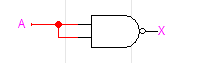
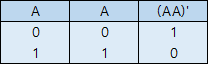
NOT 게이트 구현이 가장 쉽기 때문에, 첫 번째로 살펴보겠습니다. NAND의 입력값을 병렬로 연결하여 하나로 통일해 주었습니다. 그 결과인 (AA)' 의 진리표를 보면 (AA)'=A' 임을 알 수 있습니다. AA=A 이므로 굳이 NAND 진리표와 비교해보지 않아도 쉽게 결과를 알 수 있습니다. 따라서, 첫 번째 조건이었던 NOT 게이트를 구현하는 데 성공했습니다.
- AND
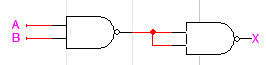
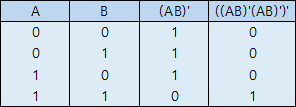
회로를 보면 NAND 게이트 2개를 사용하여 AND 게이트를 구현한 것을 확인할 수 있습니다. 이해가 어렵다면 진리표를 살펴봅시다. 먼저 첫 번째 NAND 게이트를 통해 (AB)' 라는 결과값을 얻을 수 있고, 진리표를 통해 A, B의 각 진리값에 대한 결과를 확인할 수 있습니다. 그 결과값이 다음 입력에 병렬로 들어가므로 이는 앞서 본 NOT과 같습니다. ((AB)'(AB)')'=((AB)')'=AB 이므로 NAND를 통해 AND 게이트를 구현하였습니다.
조금 더 쉽게 설명하자면 NAND(AND+NOT) + NOT 이므로, NOT끼리 상쇄되어 없어지고 AND만 남았다고 생각할 수도 있습니다.
- OR


이번에는 NAND 게이트를 3개 사용했습니다. 첫 단계에서 A'과 B'을 구하고, 이 둘을 다시 NAND 연산하는 회로입니다. ((AA)'(BB)')'=(A'B')'=A+B 이므로 마지막인 OR 게이트까지 구현하였습니다.
따라서 NAND로 AND, OR, NOT 을 모두 구현하였고, 이는 완전 집합이라고 할 수 있습니다.
NOR
NOR도 NAND와 매우 유사한 방식으로 완전 집합임을 확인할 수 있습니다. 역시 본격적으로 들어가기에 앞서 NOR 진리표를 살펴보며 기억을 되새겨 봅시다.

- NOT

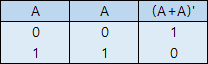
NOT 게이트의 구현은 NAND와 완전히 같습니다. 그 이유는 입력이 00일 때와 11일 때, NAND와 NOR의 진리표 상 값이 같기 때문입니다. 결국 A+A=A이므로 최종적으로 NOT 게이트가 되는 것입니다. 덕분에 아주 쉽게 첫 번째 내용을 구현하였습니다.
- AND

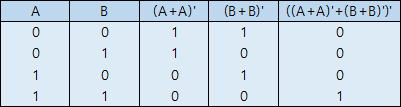
회로를 보면 NAND로 구현할 때와 달리, NOR 게이트 3개를 사용하여 AND 게이트를 구현하였습니다. 사실 자세히 보면 NAND로 OR 구현한 것과 매우 유사한 구조임을 알 수 있습니다. 이번에도 진리표를 한번 살펴봅시다. 첫 단계에서 (A+A)'=A' 과 (B+B)'=B' 을 구합니다. 그다음, 그 둘을 서로 NOR 연산하면 ((A+A)'+(B+B)')'=(A'+B')'=AB 이므로 NOR를 통해 AND 게이트를 구현하였습니다.
- OR

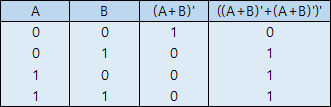
이번에는 NAND로 AND 구현할 때와 매우 유사한 것을 확인할 수 있습니다. 첫 단계에서 (A+B)' 를 구할 수 있고, 이를 병렬로 다음 NOR에 연결하였습니다. 즉, ((A+B)'+(A+B)')'=((A+B)')'=A+B 이므로 OR 게이트가 만들어졌습니다.
앞선 NAND와 마찬가지 쉽게 생각하면 NOT 게이트를 2번 통과한 것과 같습니다. NOR(=OR+NOT) + NOT 이므로 결과는 역시 OR 게이트가 됩니다.
따라서 NOR로 AND, OR, NOT 을 모두 구현하였고, 이는 완전 집합이라고 할 수 있습니다.
이렇게 완전 집합에 대해 알아봤습니다. 위의 내용을 무작정 외운다기보다는, 이렇게 NAND 또는 NOR만으로 { AND, OR, NOT }를 구현할 수 있다는 점을 기억하면 좋을 것 같습니다. 다음 포스팅은 순서상 불 대수를 정리하는 내용이 될 것 같습니다.
직접 조사해서 작성하는 글이다 보니 일부 정확하지 않은 정보가 포함되어 있을 수 있습니다.
궁금한 사항이나 잘못된 내용이 있으면 댓글로 알려주세요~
구독과 좋아요, 환영합니다!
'컴퓨터 이론 > 컴퓨터 구성' 카테고리의 다른 글
| [컴퓨터 구성] #5 NAND/NOR로 정규형(표준형) 회로 설계하기 (0) | 2022.06.21 |
|---|---|
| [컴퓨터 구성] #4 정규형(Canonical form)과 최소항(minterm)/최대항(maxterm) (2) | 2022.04.02 |
| [컴퓨터 구성] #3 불 대수(Boolean Algebra)와 기본 법칙 (0) | 2022.03.23 |
| [컴퓨터 구성] #1 논리 게이트(Logic Gates) (2) | 2022.03.09 |
| [컴퓨터 구성] #0 소개 및 기본 개념 정리 (0) | 2022.03.05 |