안녕하세요, 이번에는 불 대수에 대해 알아보겠습니다. 기본 법칙부터 여러 유용한 정리까지 많은 내용을 다룰 예정입니다.
사실 컴퓨터 구성보다는 이산수학에서 다뤄야 하는 내용이지만, 순서상으로도 그렇고, 잘 모르거나 기억이 안 날 수 있으니 다시 정리하고 공부하는 시간을 가져보겠습니다.
불 대수 (Boolean Algebra)
불 대수는 발음하기에 따라 부울 대수라고도 하는데요, 여기서는 불 대수라고 표현하겠습니다.
불 대수는 우리가 일반적으로 생각하는 수학과 달리 오직 참(1)과 거짓(0), 두 가지의 논리값만 가지는 대수입니다. 일반 대수와 규칙이 조금 다르게 적용되는 경우가 있기 때문에, 관련 법칙이나 정리를 살펴보도록 하겠습니다.
기본 법칙
지난번에 기본 게이트와 그 연산 결과를 진리표로 자세하게 알아보았는데요, 이번에는 그에 따른 여러 가지 불 대수의 기본 법칙에 대해 알아보겠습니다. 진리표가 잘 기억이 나지 않으신다면 논리 게이트 포스팅을 참고해주세요.
https://homubee.tistory.com/27
[컴퓨터 구성] #1 논리 게이트(Logic Gates)
오늘은 논리 게이트에 관해 알아보겠습니다. 논리 게이트는 컴퓨터를 구성하는 기본 요소이므로 컴퓨터 구성 공부를 위해 꼭 알아야 할 내용입니다. 자세하게 살펴보도록 하겠습니다. 논리 게
homubee.tistory.com
동일 법칙 (Identity Laws)
1. x·1=x
2. x+0=x
어떤 값에 1을 AND 연산해 주면, 그 값이 0일 때는 0이고, 1일 때는 1이라는 결과를 얻을 수 있습니다. 또한, 어떤 값에 0을 OR 연산해 주면, 그 값이 0일 때는 0이고, 1일 때는 1이라는 결과를 얻을 수 있습니다.
지배 법칙 (Domination Laws)
3. x·0=0
4. x+1=1
어떤 값에 0을 AND 연산해 주면, 결과는 그 값에 관계없이 무조건 0이 됩니다. 또한, 어떤 값에 1을 OR 연산해 주면 결과는 그 값에 관계없이 무조건 1이 됩니다.
등멱 법칙 (Idempotent Laws)
5. x·x=x
6. x+x=x
어떤 값에 그 자신을 AND 또는 OR 연산해 주면, 결과는 다시 그 스스로가 됩니다. 즉, 0·0=0, 1·1=1, 0+0=0, 1+1=1입니다. 너무 자명한 법칙이라 어렵지 않을 것 같습니다.
부정 법칙 (Negation Laws)
7. x·x'=0
8. x+x'=1
어떤 값에 그 자신의 부정한 값을 AND 연산해 주면, 0·1=0, 1·0=0이므로 항상 0이 됩니다. 반대로, OR 연산해 주면, 0+1=1, 1+0=1이므로 항상 1이 됩니다.
교환 법칙 (Commutative Laws)
9. x·y=y·x
10. x+y=y+x
AND나 OR 연산에서 순서가 바뀌더라도 그 결과는 같습니다. 즉, 0·1=1·0이고, 0+1=1+0입니다. 이는 일반 수학에서의 규칙과 같습니다.
결합 법칙 (Associative Laws)
11. x·(y·z)=(x·y)·z
12. x+(y+z)=(x+y)+z
교환 법칙과 유사하게 일반 수학에서의 규칙과 같습니다. 앞부터 순서대로 연산하거나, 뒤부터 순서대로 연산한다고 해서 결과가 달라지지는 않겠죠.
분배 법칙 (Distributive Laws)
13. x·(y+z)=x·y+x·z
14. x+y·z=(x+y)·(x+z)
분배 법칙도 일반 수학을 생각하면 쉽지만, 조금 다른 점이 있습니다. 일단 13번 법칙은 우리가 알던 분배 법칙이라 어려울 점이 없습니다. 문제는 14번인데요, 참 이상하게도 +에 분배 법칙을 사용했습니다. 이는 일반 대수에서는 성립하지 않지만 불 대수에서만 성립하는 내용입니다.
아래에서 나올 듀얼 폼으로 증명하는 것이 가장 간단하지만, 우변의 식을 그대로 전개해보아도 성립한다는 것을 알 수 있습니다. (x+y)·(x+z)=xx+xy+xz+yz이고, 이는 다시 x(1+y+z)+yz로 정리할 수 있고, 1+y+z=1이므로 x+y·z가 되어 참임을 확인할 수 있습니다.
드 모르간 법칙 (De Morgan’s Laws)
15. (x·y)'=x'+y'
16. (x+y)'=x'·y'
드 모르간 법칙은 아마 집합을 공부하셨다면 다들 익숙하실 텐데요, 그것과 같습니다. 논리식 전체에 부정 연산을 할 경우, 각 변수에 NOT 연산을 하고, AND -> OR, OR -> AND 연산으로 바꿔주어야 합니다.
이중 부정 법칙 (Double Negation Law)
17. (x')'=x
이중 부정 법칙은 같이 짝지어 나올 법칙이 없어 덩그러니 홀로 남겨졌네요. ^^ 어떤 값에 NOT 연산한 것을 다시 NOT 연산하게 되면 원래대로 돌아온다는 의미입니다.
불 대수 기본법칙 정리
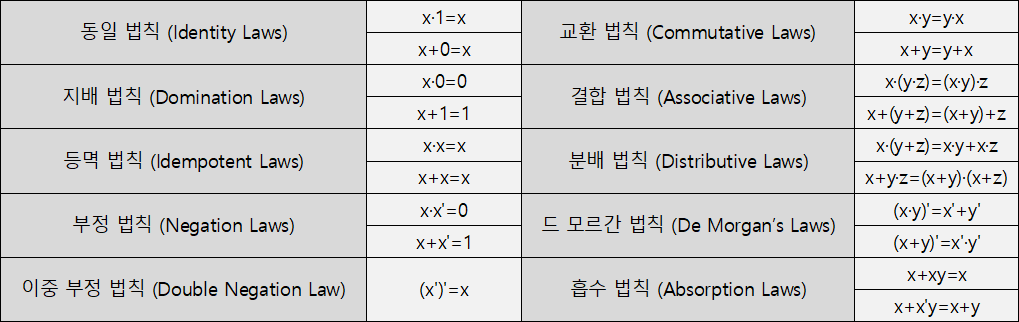
※ 흡수 법칙은 아래에 나옵니다.
이중 형태/듀얼 폼 (Dual form)
어떠한 논리식을 다음의 규칙과 같이 변형한 것을 듀얼 폼이라고 합니다. (저는 듀얼 폼이라는 용어가 익숙해서 그렇게 부르도록 하겠습니다.)
[규칙]
· 0 -> 1, 1 -> 0
· AND -> OR, OR -> AND
예를 들어 동일 법칙(1, 2번)을 다시 살펴보겠습니다. x·1=x이므로 규칙에 따라 변형하면 x+0=x입니다. 이는 또 다른 동일 법칙입니다.
하나만 더 살펴보겠습니다. 이번에는 아까 듀얼 폼 없이 복잡하게 증명했던 분배 법칙(13, 14번)입니다. x+y·z=(x+y)·(x+z)이므로 규칙에 따라 변형하면 x·(y+z)=x·y+x·z입니다. 이 역시 또 다른 분배 법칙입니다.
듀얼 폼끼리는 둘 중 하나가 참이면 다른 하나도 참이라는 점이 중요합니다. 즉, 쌍으로 묶여있는 두 법칙 중 하나만 알고 있더라도, 듀얼 폼을 통해 나머지 하나도 유도할 수 있습니다.
유용한 정리
이제는 앞에서 정리한 기본법칙을 이용해 여러 유용한 정리를 공부해봅시다. 증명하려면 발상이 조금 어려운 내용이 많아서 자세히 살펴보겠습니다.
흡수 법칙 (Absorption Laws)
1. x+xy=x
2. x+x'y=x+y
pf)
x+xy=x(1+y)=x
x+x'y=(x+x')(x+y)=x+y
첫 번째 식은 간단합니다. x 옆에 1이 AND 되어 있다고 생각하면 x(1+y)을 끌어낼 수 있고, 1+y=1이므로 결과는 x입니다. 두 번째 식이 조금 익숙하지 않을 수 있는데요, 분배 법칙을 적용한 것입니다. x+x'=1이므로 x+y만 남게 되고, 증명이 끝났습니다.
흡수 법칙도 '법칙(Law)'이라고 부르는지라 기본법칙에 넣어야 하나 고민이 많았는데, 원래 배운 것처럼 유용한 정리 부분에 남기기로 하였습니다. 개인적으로 생각할 때도, 기본법칙을 가지고 증명이 되다 보니 그편이 더 보기 좋지 않을까 싶었습니다.
합의의 정리 (Consensus Theorem)
1. ab+b'c+ac=ab+b'c
2. (a+b)(b'+c)(a+c)=(a+b)(b'+c)
pf)
ab+b'c+ac=ab+b'c+a(b+b')c=ab+b'c+abc+ab'c=ab+b'c
(a+b)(b'+c)(a+c)=(a+b)(b'+c)(a+bb'+c)=(a+b)(b'+c)(a+b+c)(a+b'+c)=(a+b)(b'+c)
이게 증명 과정에 조금 발상적인 면이 있는데요, 일단 ac에서 a(b+b')c를 만들어야 합니다. b+b'=1이므로 등식이 성립합니다. 이를 전개하고 바로 위에서 다룬 흡수 법칙을 적용하면 ab+abc=ab로, b'c+ab'c=b'c로 정리되면서 ab+b'c가 됩니다.
두 번째도 첫 번째와 거의 같습니다. 듀얼 폼이라는 점을 생각하면 첫 번째를 증명했기 때문에, 두 번째도 바로 성립한다는 점을 알 수 있지만, 그래도 한 번 살펴보도록 하겠습니다.
이번에도 같은 아이디어를 이용합니다. (a+c)에서 (a+bb'+c)를 만듭니다. 이때, bb'=0이므로 역시 등식이 성립합니다. 마찬가지로 여기에 흡수 법칙(듀얼 폼)을 적용하면 (a+b)(a+b+c)=(a+b)로, (b'+c)(a+b'+c)=(b'+c)로 정리됩니다. 따라서 최종 결과가 (a+b)(b'+c)임을 알 수 있습니다.
XOR 관련 정리
다음 내용부터는 XOR에 관련된 정리인데요, 바로 설명하면 조금 이해가 어려울 수 있을 것 같아서, 지난번에 소개하지 않았던 다음의 항등식을 소개하겠습니다.
A⊕B=AB'+A'B
XOR 게이트를 AND와 OR로 구현한 것입니다. 그냥 눈으로만 보면 이해가 어려울 수 있으니 직접 진리표를 그려왔습니다.

진리표를 읽어보면 A⊕B=AB'+A'B 라는 것을 쉽게 알 수 있습니다.
추가로 하나만 더 정리하자면 XOR 연산에서는 다음이 성립합니다.
1. x⊕x=0
2. x⊕0=x
XOR는 같은 것끼리 연산하면 그 값이 0이므로 1번은 쉽게 알 수 있습니다. 2번은 직접 값을 넣어보면 알 수 있습니다. 1⊕0=1이고, 0⊕0=0이므로 간단하게 증명되었습니다.
그럼, 이제부터 중요한 정리 2가지를 알아보겠습니다.
1. if ab'+a'b=ac'+a'c, then b=c
pf)
(a⊕b)⊕(a⊕c)=0
a⊕a⊕b⊕c=0
0⊕b⊕c=0
∴ b⊕c=0
전에 XOR 게이트는 두 진리값이 같은지 판단할 때 사용하기도 한다고 했었는데요, 여기에서 그 예시를 볼 수 있습니다. ab'+a'b=ac'+a'c 일 때, b=c를 증명해야 하므로 XOR를 사용하게 됩니다. XOR 연산 간에는 교환법칙과 결합법칙이 성립하므로 자리를 바꿔도 괜찮습니다.
따라서 괄호를 풀고 정리하면 a⊕a부분이 생기고, 앞서 설명해 드렸듯 이 부분은 정리하면 깔끔하게 사라지므로 b⊕c=0만 남습니다. XOR는 두 진리값이 서로 같을 때 출력이 0이 되므로 b=c라는 것을 증명하였습니다.
2. if a=b, then a⊕c=b⊕c
pf)
a⊕b=0
(a⊕c)⊕(b⊕c)=a⊕b⊕c⊕c=a⊕b⊕0=a⊕b
∴ a⊕c=b⊕c
이번에도 비슷합니다. 두 논리식이 같은지 증명하기 위해 XOR 연산해보겠습니다. 1번에서와 마찬가지로 c⊕c 부분이 정리되면서 a⊕b만 남습니다. a⊕b=0이므로 (a⊕c)⊕(b⊕c)=0입니다. 따라서 a⊕c=b⊕c를 증명하였습니다.
이렇게 불 대수의 기본 정리와 듀얼 폼, 그리고 여러 가지 유용한 정리에 대해 알아보았습니다. 수학적인 내용이 많아서 이게 컴퓨터인가, 수학인가 싶으실 텐데, 이 내용이 앞으로 회로 구성하는 데 있어서 기본이 되는 내용이라 꼭 이해하고 넘어가시길 바랍니다. 특히, 흡수 법칙과 합의의 정리는 맵 단순화에서도 사용되기 때문에 중요합니다.
다음번에는 Canonical form(정규형), 카르노 맵 등에 대해 다룰 예정입니다. 내용이 길고 많아서, 여러 개로 나눠서 포스팅할 생각입니다. (사실 지금 이 글도 무척 길다는 생각이 드네요;;)
직접 조사해서 작성하는 글이다 보니 일부 정확하지 않은 정보가 포함되어 있을 수 있습니다.
궁금한 사항이나 잘못된 내용이 있으면 댓글로 알려주세요~
구독과 좋아요, 환영합니다!
'컴퓨터 이론 > 컴퓨터 구성' 카테고리의 다른 글
| [컴퓨터 구성] #5 NAND/NOR로 정규형(표준형) 회로 설계하기 (0) | 2022.06.21 |
|---|---|
| [컴퓨터 구성] #4 정규형(Canonical form)과 최소항(minterm)/최대항(maxterm) (2) | 2022.04.02 |
| [컴퓨터 구성] #2 완전 집합(Complete Set) (0) | 2022.03.16 |
| [컴퓨터 구성] #1 논리 게이트(Logic Gates) (2) | 2022.03.09 |
| [컴퓨터 구성] #0 소개 및 기본 개념 정리 (0) | 2022.03.05 |