오늘은 논리 게이트에 관해 알아보겠습니다.
논리 게이트는 컴퓨터를 구성하는 기본 요소이므로 컴퓨터 구성 공부를 위해 꼭 알아야 할 내용입니다. 자세하게 살펴보도록 하겠습니다.
논리 게이트 (Logic Gates)
논리 게이트는 입력 조건을 만족했을 때, 특정한 이진 신호 0 또는 1을 만들어내는(출력하는) 하드웨어입니다.
논리 게이트에는 여러 가지 종류가 있는데요, 그림과 진리표를 함께 살펴보며 하나씩 소개하도록 하겠습니다.
논리곱 - AND
- 주어진 입력에 대해서 논리곱 연산을 수행하는 게이트
- 논리식: X=A·B
- 그림 기호

- 진리표

모두 잘 알고 있는 AND 게이트입니다. 입력이 모두 1일 때만 출력이 1이 되는 게이트입니다. 입력이 하나라도 0이면 출력이 0이 되는 게이트로 생각할 수도 있습니다.
논리합 - OR
- 주어진 입력에 대해서 논리합 연산을 수행하는 게이트
- 논리식: X=A+B
- 그림 기호

- 진리표

AND 게이트의 영원한 짝꿍! OR 게이트입니다. 입력이 하나라도 1이면 출력이 1이 되는 게이트입니다. 반대로 입력이 모두 0일 때만 출력이 0이 되는 게이트로 생각할 수도 있습니다.
논리 부정 - NOT
- 주어진 입력에 대해서 논리 부정 연산을 수행하는 게이트
- 논리식: X=A'
- 그림 기호

- 진리표

논리 부정 연산을 해주는 NOT 게이트입니다. 인버터(Inverter)라고도 합니다. 주어진 입력의 반대 값을 출력합니다.
버퍼 - Buffer
- 주어진 입력에 대해서 그대로 출력하는 게이트
- 논리식: X=A
- 그림 기호

- 진리표

버퍼는 입력을 그대로 출력하는 게이트입니다. 이런 게이트가 왜 필요할까요? 버퍼에 특별한 논리적인 의미는 없습니다. 그러나, 이론과는 달리 실제 회로에서 일어나는 다양한 문제를 고려해야 합니다. 우리가 보고 있는 0, 1이라는 값은 전압의 높낮이에 따라 결정됩니다. 이 때문에 연결된 회로가 많아지면 전기적인 문제로 오류가 발생할 수 있는데(팬 아웃: fan out), 버퍼를 통해 이러한 문제점을 해결할 수 있습니다.
부정 논리곱 - NAND
- 주어진 입력에 대해서 논리곱 연산을 한 결과에 논리 부정을 수행하는 게이트
- 논리식: X=(A·B)'
- 그림 기호

- 진리표

NAND 게이트부터는 조금 생소하실 수 있는데요. 그림을 보면 AND 게이트에 NOT(○ 모양) 게이트가 달린 모습을 살펴볼 수 있습니다. AND의 논리 부정이므로, 입력이 모두 1일 때만 출력이 0이 되는 게이트입니다.
AND와 NOT으로 구현할 수 있을 텐데, 이런 게이트가 왜 필요할까요? 그 이유는 실제 게이트를 설계할 때, AND보다 만들기 쉽기 때문입니다. 이 때문에 오히려 NAND에 NOT을 붙여 AND를 만들기도 합니다.
또한, NAND 게이트만으로 완전 집합(Complete Set)이 되기 때문에, 이것 하나만으로 다른 모든 게이트를 구현할 수 있습니다.
(완전 집합에 대해서는 추후 포스팅에서 다룰 예정입니다.)
부정 논리합 - NOR
- 주어진 입력에 대해서 논리곱 연산을 한 결과에 논리 부정을 수행하는 게이트
- 논리식: X=(A+B)'
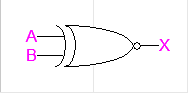
- 그림 기호
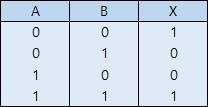
- 진리표
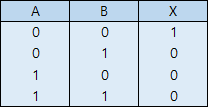
NOR 게이트도 NAND 게이트와 비슷합니다. OR+NOT이므로, 입력이 하나라도 1이면 출력이 0이 되는 게이트입니다. 이 역시 OR보다 만들기 쉽고, NOR 게이트만으로 완전 집합이 된다는 장점이 있습니다. NAND와 상당히 유사한데, 어떤 회로를 NAND 게이트만으로 구성할지, NOR 게이트만으로 구성할지는 환경에 따라 달라질 수 있습니다.
배타적 논리합 - XOR
- 주어진 입력에 대해서 배타적 논리합 연산을 수행하는 게이트
- 논리식: X=A⊕B
- 그림 기호
- 진리표
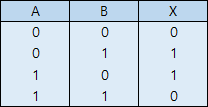
XOR 게이트는 입력에서 1의 개수가 홀수일 때만 출력이 1이 되는 게이트입니다. 즉, 3개 이상의 입력에 대해서도 XOR 연산이 가능합니다. 입력이 2개일 때를 생각해보면, 각각을 더하기(ADD) 연산하는 것과 같습니다. 또한, 두 입력이 같은지 다른지 판별할 때도 사용 가능합니다. 같을 때는 0, 다를 때는 1이 출력됩니다.
부정 배타적 논리합 - XNOR
- 주어진 입력에 대해서 배타적 논리합 연산한 결과에 논리 부정을 수행하는 게이트
- 논리식: X=(A⊕B)'
- 그림 기호
- 진리표
XOR와 NOT을 하나로 합쳐놓은 게이트입니다. 즉, 입력에서 0의 개수가 짝수일 때만 출력이 1이 되는 게이트입니다. 이 역시 두 입력이 같은지 다른지 판별할 때도 사용 가능합니다. 이 경우에는 반대로 같을 때는 1, 다를 때는 0이 출력될 것입니다.
※ XNOR를 even function으로 정의할 경우, 입력이 홀수일 때의 출력이 XOR와 같습니다. 즉, XOR+NOT으로 동작하지 않습니다. 어떤 정의를 적용하느냐에 따라 결과가 달라질 수 있는데, 이는 추후 기회가 된다면 따로 포스팅에서 다루도록 하겠습니다.
논리 게이트 정리
| 이름 | 그림 기호 | 논리식 | 진리표 |
| AND |  |
X=A·B |  |
| OR |  |
X=A+B |  |
| Inverter (NOT) |
 |
X=A' |  |
| Buffer |  |
X=A |  |
| NAND |  |
X=(A·B)' |  |
| NOR |  |
X=(A+B)' |  |
| Exclusive-OR (XOR) |
 |
X=A⊕B |  |
| Exclusive-NOR (XNOR) |
 |
X=(A⊕B)' |  |
입력 개수가 달라지면?
지금까지 소개한 내용에서는 1입력 또는 2입력 게이트에 관해서만 살펴보았는데요, 이 때문에 입력 개수를 종종 헷갈리는 경우가 있습니다.
앞서 살펴본 게이트 중 NOT과 Buffer 게이트를 제외하고는 모두 2개 이상의 입력에 대해 정의됩니다. 즉, 입력이 3개 또는 그 이상의 경우에도 앞서 설명해 드린 정의를 그대로 적용하시면 됩니다. (XNOR만 주의) 예를 들어 AND는 입력이 모두 1일 때만 출력이 1이 되는 게이트이므로 110은 0이지만, 111은 1이라는 결과를 얻을 수 있습니다.
이렇게 기본적인 논리 게이트를 알아봤습니다. 직접 그림도 그리고, 표도 만들려니 무척이나 힘드네요. 앞으로 다룰 내용에서 가장 기초가 되는 내용이니 잘 기억하시기 바랍니다.
다음번에는 완전 집합(Complete Set)에 대해 알아보겠습니다!
직접 조사해서 작성하는 글이다 보니 일부 정확하지 않은 정보가 포함되어 있을 수 있습니다.
궁금한 사항이나 잘못된 내용이 있으면 댓글로 알려주세요~
구독과 좋아요, 환영합니다!
'컴퓨터 이론 > 컴퓨터 구성' 카테고리의 다른 글
| [컴퓨터 구성] #5 NAND/NOR로 정규형(표준형) 회로 설계하기 (0) | 2022.06.21 |
|---|---|
| [컴퓨터 구성] #4 정규형(Canonical form)과 최소항(minterm)/최대항(maxterm) (2) | 2022.04.02 |
| [컴퓨터 구성] #3 불 대수(Boolean Algebra)와 기본 법칙 (0) | 2022.03.23 |
| [컴퓨터 구성] #2 완전 집합(Complete Set) (0) | 2022.03.16 |
| [컴퓨터 구성] #0 소개 및 기본 개념 정리 (0) | 2022.03.05 |