오늘은 카르노 맵에 대해 알아보겠습니다. 또한, 변수 개수에 따라 식 간소화 과정도 함께 살펴볼 예정입니다.
카르노 맵은 조금 내용이 많습니다. 생소하고 어려울 수 있지만 역시 불대수에 기반하고 있으므로 천천히 생각해보면 이해하실 수 있습니다.
식 간소화 (Simplification)
예를 들어 f=a+ad'+abc+ac'ef+ahj라는 식이 있다고 해봅시다. 이걸 그대로 회로로 만들려면 너무 힘들겠죠? 정리하면 간단하게 f=a로 만들 수 있으니, 식을 간소화하자는 것입니다.
식을 간소화하는 방법에는 여러 가지가 있습니다. 항을 줄이는 방법, 상수를 없애는 방법, 항을 추가하는 방법 등 다양합니다. 이때에는 불 대수가 활용되는데, 주로 흡수 법칙, 합의의 정리 등을 활용하면 쉽게 식을 간소화할 수 있습니다.
항을 추가하는 방법이 식 간소화 방법이라는 것에 놀라실 수도 있는데, 이 역시 합의의 정리를 응용한 것입니다. f=ab+b'd'+ac'd'이라는 식이 있다면, ab+b'd'=ab+b'd'+ad'이므로 +ad'를 추가할 수 있고 ad'+ac'd'=ad'이므로 식이 간소화되는 것을 확인할 수 있습니다.
무관항 (Don't care condition)
완전히 확정되지 않은 함수(Incompletely specified functions)라고도 합니다. 무관항은 Don't care라는 말 그대로 신경 쓰지 않는다는 것입니다. 이때는 변수를 0이나 1 중 임의의 값으로 설정하여 편한 대로 식을 조작할 수 있습니다.
이런 항이 존재하는 이유는 입력이라든지 기타 상황에 따라 그 케이스가 벌어지지 않을 수 있기 때문입니다. 있을 수 없는 경우이므로 자유롭게 값을 설정해도 되겠죠? 또는 예를 들어 6개의 이진 데이터가 있는데, 4bit에 저장하려면 2자리가 남겠죠? 이럴 때도 사용하게 됩니다.
이제 지금까지 배운 내용을 활용하여 카르노 맵에 대해 배워보겠습니다.
카르노 맵 (Karnaugh Map)
카르노 맵은 논리식을 간소화하는 방법의 하나입니다. 앞서 보았듯이 직접 불 대수를 활용하여 식을 정리하기에는 어려움이 있기 때문에, 이를 해결하기 위해 만들어진 일종의 식 간소화 기법이라고 생각할 수 있습니다. 카르노 맵을 이용하면 쉽고 직관적으로 논리식을 간소화할 수 있습니다.
카르노 맵을 통해 얻은 논리식이 가장 간소화된 최소 비용의 식인지는 알 수 없으므로, 문제를 풀 때 최소 비용의 식을 구하라고 한다면, 카르노 맵 적용 이후 다시 한번 체크해보아야 합니다. 카르노 맵은 표준화된 방법으로 식 간소화가 가능하다는 점에서 의의가 있습니다.
카르노 맵을 그리는 방법을 알아보겠습니다. 먼저 변수 개수에 따라 나올 수 있는 경우를 모두 표에 표현합니다. 각 변수는 0 또는 1의 값을 가지므로, 2변수이면 4칸, 3변수이면 8칸의 카르노 맵이 그려집니다.
여기에 간소화해야 할 정규형 논리식을 보고, 최소항 전개식이라면 해당 칸에 1을, 최대항 전개식이라면 해당 칸에 0을 채우고, 나머지 칸에는 반대되는 숫자를 채워줍니다. 이제 카르노 맵을 다 그렸으니 간소화만 남았습니다.
(최대항 전개식이고 숫자가 주어지지 않았다면, 항을 부정한 후, 해당 칸에 0을 채워야 합니다. 이는 아래에서 다시 설명하도록 하겠습니다.)
같은 숫자끼리 2의 제곱수 단위로 직사각형 모양으로 묶으면, 변하지 않는 고정값을 찾을 수 있는데요, 이렇게 모든 0 또는 1을 묶어 고정값을 찾아 식으로 표현하면 간소화 식을 구할 수 있습니다.
0을 묶으면 합의 곱(POS) 기준으로 간소화한 식이 되고, 1을 묶으면 곱의 합(SOP) 기준으로 간소화한 식이 됩니다.
이렇게 구구절절 설명해놓은 것으로는 이해가 어려울 테니, 변수의 개수에 따라 2변수에서 5변수까지 모두 한번 직접 살펴보도록 하겠습니다.
2변수 카르노 맵
변수 a, b를 가지고 카르노 맵을 그려봅시다. f=Σm(0, 1)=a'b'+a'b이라고 해보겠습니다. 그냥 불 대수만 가지고도 쉽게 f=a'이라는 것을 알 수 있지만 카르노 맵을 한번 활용해보겠습니다.

위와 같이 카르노 맵을 그릴 수 있습니다. 0, 1로 각 변수의 상태를 표현합니다. 0이 부정(')이고, 1이 원래 값입니다. 수식을 보면 a'b'과 a'b로 이루어져 있으므로 00인 자리와 01인 자리에 1을 채워 넣습니다. 나머지 자리는 0을 채우면 됩니다. 여기에서 인접해 있는 두 1을 묶으면 다음과 같습니다.

묶여있는 두 칸을 보면 a'은 고정이고 b'과 b는 변하는 값임을 알 수 있습니다. 여기에서 고정된 값만 남기면 a'만 남게 되고, 이것이 그대로 간소화 식이 되어 f=a'이 됩니다.
변하는 값을 없애고 고정된 값만 남긴다는 게 무슨 의미인지 잘 이해가 안 될 수 있는데, 변한다는 것은 어느 쪽이든 관계없다는 뜻이고, 고정되어 있다는 것은 그 값만 된다는 뜻입니다. 위의 식은 f=a'b'+a'b이므로 f=a'(b'+b)로 정리되어 f=a'이 됩니다. 즉, b가 0이든 1이든 관계없이 a의 값만이 의미 있는 부분입니다.
이러한 구조는 다변수 카르노 맵에서도 똑같이 나타납니다. 변수가 늘어나더라도 같은 원리로 카르노 맵을 통해 간단하게 식을 간소화할 수 있습니다.
3변수 카르노 맵
이번에는 변수 a, b, c를 가지고 카르노 맵을 그려보겠습니다. f=Σm(1, 5, 6, 7)=a'b'c+ab'c+abc'+abc로 해보도록 하겠습니다. 아직은 불 대수로 정리할 만하지만, 카르노 맵을 이용하면 훨씬 편합니다. 먼저 아까와 같은 방식으로 표를 그리고 내용을 채워 넣습니다.

이번에도 마찬가지로 1끼리 묶어보도록 하겠습니다.

다시 한번 설명해 드리자면, 모든 1을 최소 한 번씩 묶여야 간소화할 수 있습니다. 파란색으로 한 번 묶어주고, 주황색으로 한 번 묶어주면 모든 1을 다 묶어줄 수 있습니다.
파란색 묶음을 보면, b'c가 고정이고 a가 바뀝니다. 주황색 묶음을 보면, ab가 고정이고 c가 바뀌는 것을 확인할 수 있습니다. 따라서 간소화 결과는 f=ab+b'c라는 것을 간단하게 구해냈습니다.
여기에서 재미있는 사실을 알 수 있는데요. 아까 '최소' 한번 묶어야 한다고 했는데, 이 말은 그 이상으로 묶어도 된다는 것입니다. 그렇다면 다음과 같이 묶어보면 어떨까요?

초록색으로 한 번 더 묶어보았습니다. 초록색 묶음은 ac가 고정이므로 f=ab+b'c+ac가 됩니다. 이게 무슨 의미인가? 할 수 있는데, 잘 살펴보시면 이전에 불 대수 법칙에서 보았던 합의의 정리를 확인할 수 있습니다. 이에 따라 f=ab+b'c로 다시 정리되므로, 최소 비용의 식을 구하려면 굳이 한번 묶은 1을 또 묶을 필요는 없습니다.
카르노맵 번호 표기
매번 숫자를 가지고 식을 세운 후 다시 표를 채우려면 무척 번거롭기 때문에, 표 위치에 따른 숫자를 외우는 것이 편합니다. 앞선 2변수와 3변수 모두 살펴보면 다음과 같습니다.
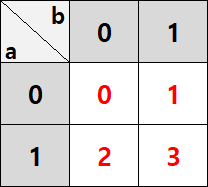
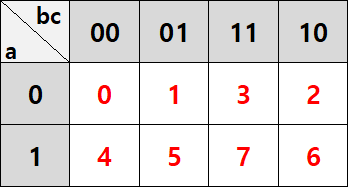
f=Σm(~~)와 같이 숫자 표기가 되어 있다면 바로 해당 숫자에 해당하는 위치에 1을 채워 넣으면 됩니다. f=ΠM(~~) 형태로 주어진다면 해당 위치에 0을 채워 넣으면 됩니다.
하나 더 예시를 살펴보도록 하겠습니다. 이번에는 f=Σm(0, 1, 2, 3, 4, 6)입니다. 위의 방법을 사용하여 바로 표를 채우도록 하겠습니다.
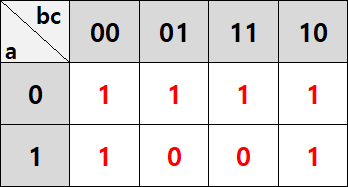
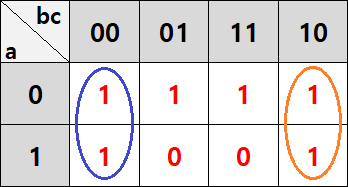
표를 채우는 것은 어렵지 않으셨을 것 같은데, 묶을 때 조금 고민이 될 것 같습니다. 일단 오른쪽과 같이 양 끝에 있는 두 1을 세로로 묶어봅시다. 그다음은 어떻게 묶으면 좋을까요?
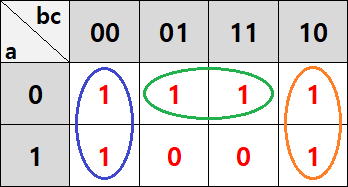
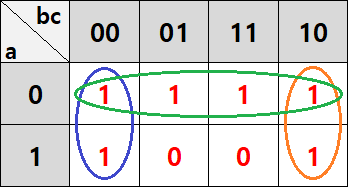
1, 3번 자리만 묶었다면 f=b'c'+bc'+a'c입니다. 그런데, 가로로 4개의 1이 눈에 들어옵니다. 4개를 전부 묶어보겠습니다. 이 경우에도 똑같이 고정된 값으로 만들어 줄 수 있습니다. a'이 고정이고 b, c는 바뀌므로, f=b'c'+bc'+a'이 되었습니다.
즉, 겹치는 부분이 있더라도 더 여러 개를 묶을 수 있다면 한꺼번에 묶는 것이 더 적은 비용의 식을 만드는 방법입니다. 아까 설명했듯이 개수가 2의 제곱수가 되도록 묶되, 직사각형 모양으로 묶어지는 경우에만 가능합니다.
예를 들어 ㅜ모양으로 1이 있더라도 4개이므로 2의 제곱수 조건은 충족하지만, 직사각형이 아니므로 한 번에 묶을 수 없고, 3번에 나눠서 묶어야 합니다. 위의 식을 다시 보니 b'c'+bc'=c'으로 정리된다는 것이 바로 눈에 들어오는데요. 처음부터 다시 한번 제대로 묶어보겠습니다.
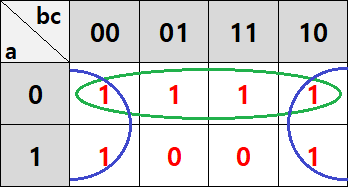
상하좌우의 인접한 숫자도 한꺼번에 묶어줘야 합니다. 가장 왼쪽의 부분을 가장 오른쪽에 붙여놓은 것과 같습니다. 즉, 카르노 맵으로 제대로 간소화 식을 구했다면, 위와 같이 파란색으로 4개가 묶이므로 c'값까지 적용해서 f=a'+c'으로 정리할 수 있습니다.
4변수 카르노 맵
4변수 카르노 맵은 다음과 같이 그리면 됩니다. (변수는 a~d를 사용)

이번에는 f=Σm(0, 1, 2, 5, 8, 9, 10, 11)+Σd(3, 13, 15)를 카르노 맵으로 그려 간소화해보도록 하겠습니다. d는 Don't care condition을 의미합니다. 이는 X로 표시합니다.
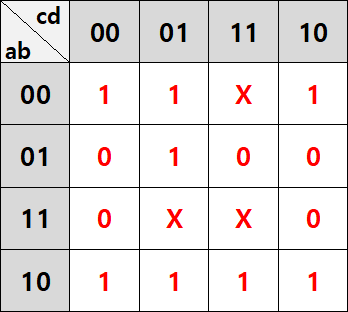
무관항까지 포함된 카르노 맵을 그려보았습니다. 아까 설명했듯이 X는 마음대로 바꿀 수 있기 때문에, 적당히 간소화하기 좋게 바꾸고 묶어보겠습니다.

3, 13 자리는 1로, 15 자리는 0으로 바꾸면 아주 예쁘게 묶을 수 있습니다. 파란색은 b'이 고정이고, 초록색은 c'd가 고정이므로 간소화 식은 f=b'+c'd입니다. X의 값을 다르게 정했다면 다른 식이 나오겠죠? 따라서 무관항이 포함된 식은 그 값을 잘 설정해야 적은 비용의 식을 구할 수 있습니다.
아까 설명했지만, 여기에서 0을 기준으로 묶으면 역으로 POS 식을 구할 수도 있습니다.
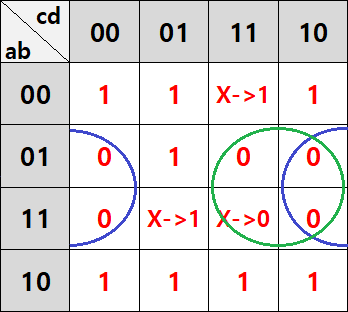
위와 같이 묶을 수 있는데요, 여기에서 주의할 점이 있습니다. 0을 묶게 되면 항을 만들 때 1을 묶었을 때와 반대로 부정 연산 후에 구해야 합니다.
즉, 파란색에서 b+d'이 아니라 b'+d가 되고, 초록색에서는 b+c가 아니라 b'+c'이 됩니다. 따라서 간소화 식은 f=(b'+d)(b'+c')입니다. 전개해보면 f=b'+c'd로 위의 식과 같은 결과를 얻을 수 있습니다.
부정 연산을 되는 이유는 간단합니다. POS 간소화 식을 구할 때는 SOP 식의 듀얼 폼을 구하는 방식이기 때문입니다. 듀얼 폼은 이전 불 대수 포스팅에 설명해두었으니 참고하시길 바랍니다.
https://homubee.tistory.com/31
[컴퓨터 구성] #3 불 대수(Boolean Algebra)와 기본 법칙
안녕하세요, 이번에는 불 대수에 대해 알아보겠습니다. 기본 법칙부터 여러 유용한 정리까지 많은 내용을 다룰 예정입니다. 사실 컴퓨터 구성보다는 이산수학에서 다뤄야 하는 내용이지만, 순
homubee.tistory.com
부정 연산을 하지 않고 그대로 가져와 식을 세우면 f=bd'+bc입니다. 하지만 우리가 원하는 것은 f가 아니라 f'입니다.(0을 기준으로 묶었으므로) 따라서, 전체에 부정 연산을 하면 f'=(bd'+bc)'=(bd')'(bc)'=(b'+d)(b'+c') 임을 알 수 있습니다. 즉, 처음 구한 식의 듀얼 폼이 됩니다.
5변수 카르노 맵
사실 5변수부터는 카르노 맵을 쓰는 것이 거의 의미가 없는데요, 그래도 간단하게만 살펴보겠습니다. 이때는 4변수 카르노 맵을 두 번 사용해야 합니다. 변수를 a~e라고 하면 a'(a=0)일 때와, a(a=1)일 때의 카르노 맵을 한 번씩 그리면 됩니다. 말로는 이해가 어려울 수 있으니 직접 그려보도록 하겠습니다.
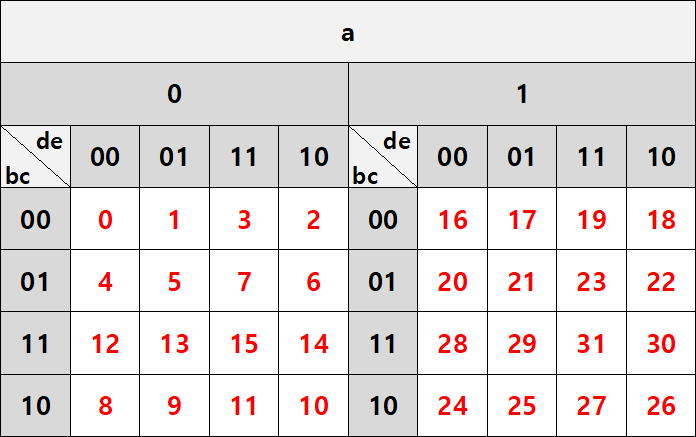
그냥 단순히 여기에서 끝이고 위에서와 같은 방식으로 간소화할 수 있다면 좋겠지만, 5변수는 새로운 상황을 하나 더 고려해야 합니다. a값은 바뀌고, 나머지 값이 고정인 경우가 생기기 때문에, 두 개의 카르노 맵을 겹쳐 보아야 합니다.
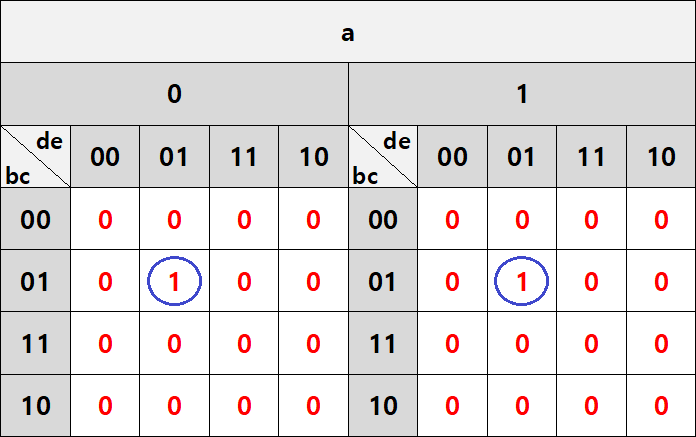
예를 들어, f=Σm(5, 21)이면 5와 21이 따로따로 묶이는 것이 아니라, 겹쳐보면 같은 자리이므로 위와 같이 묶어주어야 한다는 것입니다. 5, 21을 묶으면 b'cd'e는 고정이고 a가 바뀌므로, f=b'cd'e로 정리할 수 있습니다.
이처럼 두 개의 카르노 맵을 중첩하여 묶어주어야 하므로 빠뜨리기도 쉽고, 여러모로 복잡하고 어렵습니다. 따라서, 5변수부터는 그냥 불 대수를 이용하여 정리하는 것을 추천합니다.
번외편: 모두 1이라면?
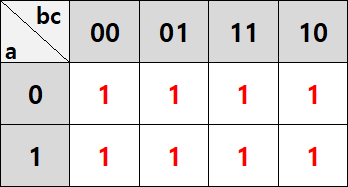
위와 같이 모두 1인 경우라면 어떻게 하면 될까요? 똑같습니다. 전체가 8개이므로 2의 제곱수이고, 직사각형 모양이니 한 번에 묶을 수 있습니다. 다만, 고정되는 값이 없으므로 그냥 f=1이 됩니다. 반대로 모두 0이라면 f=0이 됩니다.
오늘은 식 간소화와 카르노 맵에 대해 알아보았습니다. 아직은 카르노 맵 그리는 것이 익숙하지 않고 힘들 수도 있지만, 자꾸 연습해서 익혀 나갑시다. 이 역시 추후 회로를 만들려면 꼭 필요한 내용이니까 잘 숙지해두시기 바랍니다.
직접 조사해서 작성하는 글이다 보니 일부 정확하지 않은 정보가 포함되어 있을 수 있습니다.
궁금한 사항이나 잘못된 내용이 있으면 댓글로 알려주세요~
구독과 좋아요, 환영합니다!
'컴퓨터 이론 > 컴퓨터 구성' 카테고리의 다른 글
| [컴퓨터 구성] #8 n-bit 가산기 설계하기 (Ripple-carry Adder/Carry-lookahead Adder) (0) | 2022.09.24 |
|---|---|
| [컴퓨터 구성] #7 반가산기(Half Adder), 전가산기(Full Adder) (0) | 2022.09.10 |
| [컴퓨터 구성] #5 NAND/NOR로 정규형(표준형) 회로 설계하기 (0) | 2022.06.21 |
| [컴퓨터 구성] #4 정규형(Canonical form)과 최소항(minterm)/최대항(maxterm) (2) | 2022.04.02 |
| [컴퓨터 구성] #3 불 대수(Boolean Algebra)와 기본 법칙 (0) | 2022.03.23 |