오늘은 지난번 반가산기, 전가산기에 이어, n-bit 가산기를 설계하는 내용을 공부해보겠습니다. Ripple-carry Adder와 Carry-lookahead Adder, 2가지 종류의 가산기를 모두 만들어볼 예정입니다.
이전 포스팅과 연결되는 내용이니 필요하시다면 아래의 링크를 참고해주세요.
https://homubee.tistory.com/43
[컴퓨터 구성] #7 반가산기(Half Adder), 전가산기(Full Adder)
오늘은 반가산기와 전가산기를 공부해보겠습니다. 컴퓨터가 해야 할 연산 가운데 가장 중요한 것 중 하나가 바로 덧셈 연산입니다. 가산기는 이 덧셈 연산을 해주는 장치인데요, 가산기의 기본
homubee.tistory.com
n-bit 가산기 설계하기
Ripple-carry Adder
이전 포스팅에서 만들었던 가산기를 이용하여 n-bit 가산기를 만들어보겠습니다. 이번 포스팅에서는 기존의 x, y, z에서 변수명을 조금 바꿔서 A, B, Cin를 사용하도록 하겠습니다. c는 Cout으로 부르도록 하겠습니다.
n-bit 가산기는 단순하게 n개의 전가산기를 연결하여 만들 수 있습니다. 이전 비트의 Cout이 다음 비트의 Cin이 되도록 연결하면 됩니다. 4bit 가산기를 한번 만들어보았는데요, 완성된 회로는 다음과 같습니다.
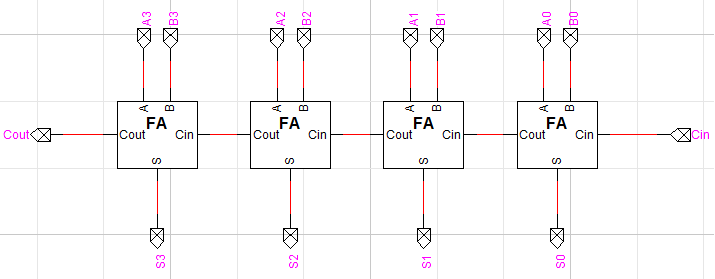
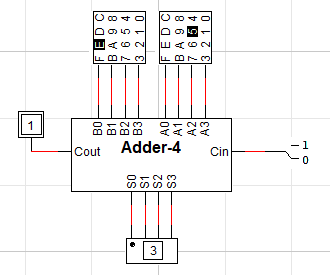
왼쪽 사진이 완성된 4bit Adder의 회로입니다. 4bit이므로 입력 A, B 역시 4bit로 들어오게 됩니다. 출력은 Cout을 포함하면 5bit, 단순 덧셈 결과만 보면 4bit입니다.
오른쪽 사진을 보면 연산을 잘 수행하는 것을 확인할 수 있습니다. 입력 A는 5(0101), B는 E(1110)이므로 S는 3(0011), Cout은 1이 나오는 것입니다.
이렇게 구현한 방식의 가산기를 Ripple-carry Adder (RCA) 라고 합니다. 우리말로는 순차 자리 올림 가산기라고 부르기도 합니다. 저는 편의상 영문명을 사용하도록 하겠습니다.
리플 캐리 가산기는 간단하게 전가산기를 통해 구현할 수 있다는 장점이 있지만, 비트 수가 늘어날수록 연산속도가 느려진다는 단점이 있습니다. 그 이유는 입력에서 알 수 있습니다. 캐리가 입력으로 들어오기 때문에, 이전 비트에서 캐리가 계산되어 입력될 때까지 상위 비트의 가산기는 아무것도 하지 못하고 대기해야 합니다. 이 과정에서 딜레이가 발생하면서 연산 효율을 저하하는 문제점이 발생합니다.
Carry-lookahead Adder
앞선 문제점을 개선한 것이 바로 Carry-lookahead Adder (CLA) 입니다. 자리 올림 예측(선견) 가산기라고도 부릅니다. 이번에도 편의상 영문명으로 부르도록 하겠습니다.
캐리 룩어헤드 가산기는 S와 C 대신 G와 P를 입력으로 가집니다. G는 Generate(생성), P는 Propagate(전달)의 약자입니다. G와 P는 다음과 같이 정의됩니다. (i는 자릿수를 의미합니다.)
- Gi = Ai·Bi
- Pi = Ai⊕Bi
G는 반드시 캐리를 '생성'하는 경우이고, P는 이전 캐리를 '전달'받은 경우 캐리를 생성하는 경우입니다. 이것만 봐서는 잘 감이 오지 않는데, 여기에서 다음의 식이 성립함에 따라 Ci(i번째 캐리)를 구할 수 있습니다.
- Ci = Gi-1 + Pi-1Ci-1
위 식이 성립하는 이유를 잘 생각해봅시다. G는 A와 B의 AND 연산 결과이므로 둘 다 1일 때만 1입니다. 즉, A, B를 더해서 캐리가 생길 때 1이 됩니다. P는 A, B 중 하나에 1이 있을 때 1이 됩니다. 이때 이전 비트에 캐리가 있다면 이 전달된 P 값과 더해줄 수 있고, 이 경우에도 캐리가 생기므로 AND 연산을 해준 것입니다. 마지막으로 전체를 OR 연산하여 묶어주면 원하는 캐리 값을 구할 수 있습니다.
여기서 중요한 것은 이 식이 점화식 형태를 가지고 있다는 점입니다. 이를 활용하면 모든 캐리를 오직 최초에 입력으로 들어올 Cin(또는 C0)으로부터 구할 수 있습니다. 실제 식으로 나타내보면 다음과 같습니다.
- C1 = G0 + P0C0
- C2 = G1 + P1C0 = G1 + P1(G0 + P0C0) = G1 + G0P1 + P1P0C0
- C3 = G2 + P2C1 = ... = G2 + G1P2 + G0P2P1 + P2P1P0C0
- C4 = G3 + P3C2 = ... = G3 + G2P3 + G1P3P2 + G0P3P2P1 + P3P2P1P0C0
G나 P값은 A, B로부터 바로 구할 수 있으므로 최초 입력값을 통해 딜레이 없이 덧셈 연산을 수행할 수 있습니다.
캐리 룩어헤드 가산기를 만들기 위한 변형된 Full Adder(1-bit)는 다음과 같습니다.
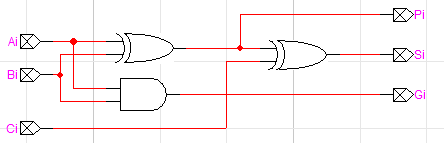
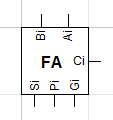
이를 확장하여 n-bit 가산기를 만들어보겠습니다.
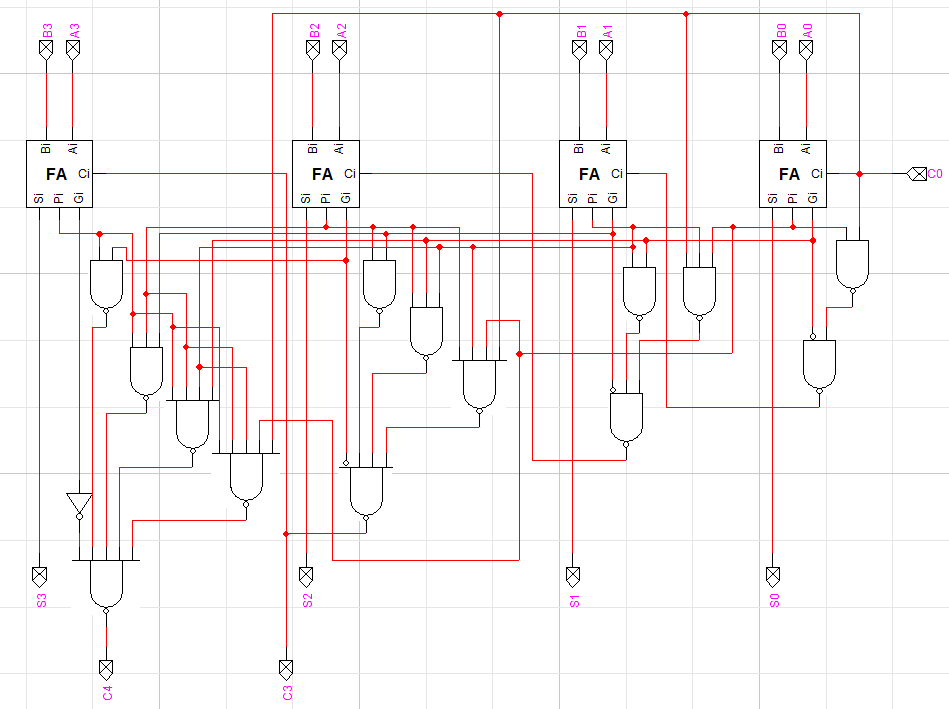

왼쪽을 보면 무척 복잡한 회로를 확인할 수 있습니다. 위에서 구한 C1~4까지 식을 그대로 회로로 구현한 것입니다. 구조는 다르지만 계산 결과는 아까와 같이 잘 출력되는 것을 확인할 수 있습니다. C3는 왜 따로 있는지 의아해하실 수 있는데, 나중에 사용할 예정이니 지금은 잠시 무시하셔도 됩니다.
2-level 게이트의 time delay를 d라고 하면, 4bit 기준으로 리플 캐리 가산기는 4번의 FA를 순차적으로 거치므로 약 4d만큼 발생합니다. 반면에, 캐리 룩어헤드 가산기는 처음 P와 G값을 계산하는데 d, 각 C값을 계산하는데 d, C값을 통해 S를 계산하는데 d만큼 소요되므로 약 3d만큼 발생합니다. (정확한 delay를 구하려면 복잡하므로 이해를 돕기 위해 대략적인 수치를 이용했습니다.)
4d와 3d이므로 별 차이가 안 난다고 생각할 수도 있는데, 캐리 룩어헤드 가산기의 진가는 비트 수가 커질 때 드러납니다. 예를 들어 64bit 가산기가 있다고 해봅시다. 리플 캐리 가산기는 64d가 발생할 것입니다. 하지만, 캐리 룩어헤드 가산기는 그대로 3d입니다. 항상 3d만큼만 딜레이가 발생하기 때문에 비트 수가 커질수록 지연 시간에서 큰 이득입니다.
왼쪽 회로 이미지를 보면 알 수 있듯이 시간상으로는 이득이지만, 이는 하드웨어적으로 해결하는 방식이기 때문에 비트수가 늘어날수록 구현이 어렵습니다. 따라서 두 방식의 가산기를 절충하여 사용하게 됩니다. 4bit의 캐리 룩어헤드 가산기를 리플 캐리 방식으로 연결하여 16bit 가산기를 만드는 형태입니다. 다음의 회로가 그 예시입니다.
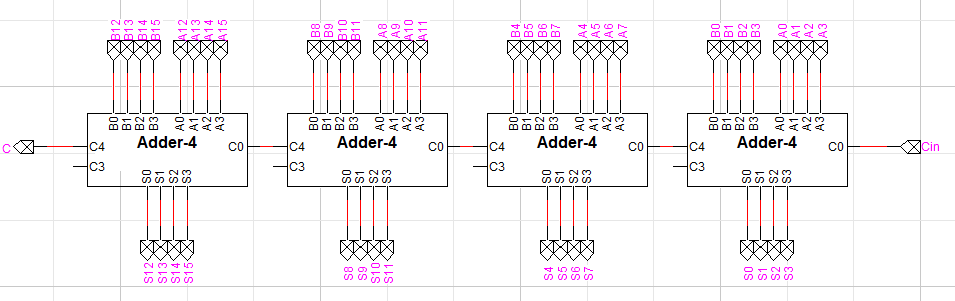
두 방식을 절충하여 만든 16-bit 가산기입니다. 각 4bit 가산기에서 3d만큼 지연되고, 4번을 순차적으로 거치므로 총 12d의 딜레이가 발생합니다. 리플 캐리 가산기로만 구현하면 16d이므로 4d만큼 이득입니다. 이 가산기가 덧셈 연산을 잘 수행하는지는 다음 내용을 다룬 후 같이 살펴보도록 하겠습니다.
상태 변수 추가하기
가장 기본적인 가산기는 덧셈 연산만 수행하면 되지만, 우리는 조금 더 기능을 확장해보도록 합시다. 몇 가지 상태 변수가 추가되면 더욱 유용한 가산기를 만들 수 있습니다.
가산기에 자주 필요한 상태 변수는 Cout, Overflow, Sign, Zero가 있습니다. 이중 Cout은 이미 구현되어 있으므로 나머지를 살펴보겠습니다. 또한, 각각은 간단히 순서대로 C V S Z로 표시하도록 하겠습니다.
Overflow는 값이 메모리 용량보다 클 때 발생하는 일종의 컴퓨터 오류입니다. 이는 마지막 비트와 그 이전 비트의 캐리를 XOR 연산하여 구할 수 있습니다. 본 포스팅에서 만든 가산기는 2의 보수 규칙으로 연산을 수행하기 때문에 이렇게 오버플로우 체크를 해줍니다. 아까 만들어두었던 C3 포트가 여기에서 사용됩니다.
아직 보수에 대해 다루지 않았기 때문에 이해가 어려우실 수 있습니다. 간단히 설명하자면, 최상위 비트를 부호 비트로 하여, 0이면 양수, 1이면 음수가 됩니다. 따라서 최상위 비트 이전 비트에서 캐리가 발생하여 오버플로우가 발생하거나, 더하는 두 값의 최상위 비트가 모두 1이어서 오버플로우가 발생하는 경우를 체크하는 것입니다. 추후에 포스팅으로 다룰 예정이니 그때 더 자세히 설명하도록 하겠습니다.
Sign은 부호 비트를 의미합니다. 최상위 비트를 부호 비트로 사용하므로 해당 비트를 체크하면 됩니다. 앞서 설명했듯이 0이라면 양수, 1이라면 음수를 의미합니다.
Zero는 모든 비트가 0임을 의미합니다. 이는 연산 결과에 NOR 게이트를 연결하여 간단하게 구할 수 있습니다.


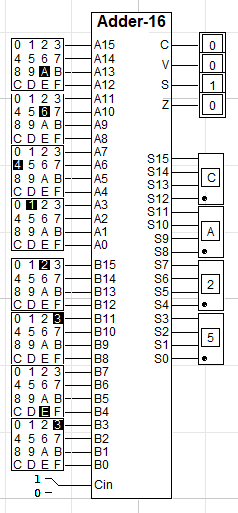
이렇게 상태 변수까지 추가하여 가산기를 완성했습니다! 연산 결과도 잘 출력되는 것을 확인할 수 있습니다. 참고로 Zero의 경우 input이 16개인 NOR 게이트가 따로 없어서 4bit마다 NOR 연산 후 그 결과들을 AND 게이트로 연결하여 체크하였습니다.
번외편 : BCD Adder
BCD는 Binary-Coded Decimal(이진화 십진법)의 약자로, 2진수를 이용해 10진법으로 표기하는 것을 의미합니다. 우리가 실제로 사용하는 것은 10진법이다 보니 BCD가 필요한 경우도 여럿 있는데, 이를 이용한 가산기를 만들어보겠습니다.
먼저 BCD에서 숫자를 어떻게 표기하는지 알아봅시다.

0부터 9까지 이진수로 일대일대응 시킨 간단한 방식입니다. 예를 들어 387이라면 0011 1000 0111 로 표기하면 됩니다.
2+3 같은 작은 숫자 덧셈은 그대로 5(0101)가 나오므로 별 상관이 없지만, 더한 결과가 10을 넘어가면 BCD 범위를 벗어납니다. 이때, 6(0110)을 더하면 다시 BCD 코드로 변환할 수 있습니다.
예를 들어 11은 1011인데요, 여기에 0110을 더하면 1 0001이 되므로 십의 자리 숫자 1과 일의 자리 숫자 1을 다시 구할 수 있습니다. 어떤 원리일까요?
BCD는 4bit로 표시하므로 0~15까지 표현할 수 있습니다. 따라서, 10 이상의 어떤 숫자에 6을 더하게 되면 4bit로는 16을 표현할 수 없으므로 오버플로우가 발생하고 16만큼 빼주는 효과가 발생합니다. 즉, 6을 더하고 16을 빼주었으므로 총 10만큼 빼주어 십의 자리와 일의 자리를 분리할 수 있는 것입니다. 결과적으로 캐리는 십의 자리 숫자가 되고, 남은 숫자가 일의 자리가 됩니다.
이에 따라 10을 넘어가는 경우의 진리표와 카르노 맵을 통해 식을 구하면 됩니다. 단순하므로 진리표는 생략하고 카르노 맵만 본다면, 1010부터 그 이상 숫자에 해당하는 모든 칸에 1을 채워 넣고 묶어주면 됩니다.
정리하면 S3S2+S3S1이 나오는데, 여기서 주의할 점은 C4까지 더해주어 f=C4+S3S2+S3S1이라는 점입니다. 4bit 가산기라도 캐리를 고려하면 그 결과는 5bit로 출력되므로 캐리가 발생하는 경우에도 6을 더해주어야 합니다.

따라서, 완성된 BCD Adder는 다음과 같습니다.

9+5=14를 잘 계산하고 있는 것을 확인할 수 있습니다.
n-bit 가산기에 대해 알아보고 직접 만들어보았습니다. 나중에 CPU 만들 때 활용되므로 잘 기억해두시기를 바랍니다.
직접 조사해서 작성하는 글이다 보니 일부 정확하지 않은 정보가 포함되어 있을 수 있습니다.
궁금한 사항이나 잘못된 내용이 있으면 댓글로 알려주세요~
구독과 좋아요, 환영합니다!
'컴퓨터 이론 > 컴퓨터 구성' 카테고리의 다른 글
| [컴퓨터 구성] #9 플립플롭(Filp-Flop)과 그 종류 (SR, D, JK, T) (2) | 2023.05.01 |
|---|---|
| [컴퓨터 구성] #7 반가산기(Half Adder), 전가산기(Full Adder) (0) | 2022.09.10 |
| [컴퓨터 구성] #6 카르노 맵 (Karnaugh Map)과 식 간소화 (2) | 2022.08.20 |
| [컴퓨터 구성] #5 NAND/NOR로 정규형(표준형) 회로 설계하기 (0) | 2022.06.21 |
| [컴퓨터 구성] #4 정규형(Canonical form)과 최소항(minterm)/최대항(maxterm) (2) | 2022.04.02 |